A.
Permutation p is an ordered set of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. We'll denote the i-th element of permutation p as pi. We'll call number n the size or the length of permutation p1, p2, ..., pn.
The decreasing coefficient of permutation p1, p2, ..., pn is the number of such i (1 ≤ i < n), that pi > pi + 1.
You have numbers n and k. Your task is to print the permutation of length n with decreasing coefficient k.
In a single line print n space-separated integers: p1, p2, ..., pn — the permutation of length n with decreasing coefficient k.
If there are several permutations that meet this condition, print any of them. It is guaranteed that the permutation with the sought parameters exists.
3 2 1 构造题;
#include #include #include #include #include #include #include #include
Petya and Vasya are playing a game. Petya's got n non-transparent glasses, standing in a row. The glasses' positions are indexed with integers from 1 to n from left to right. Note that the positions are indexed but the glasses are not.
First Petya puts a marble under the glass in position s. Then he performs some (possibly zero) shuffling operations. One shuffling operation means moving the glass from the first position to position p1, the glass from the second position to position p2 and so on. That is, a glass goes from position i to position pi. Consider all glasses are moving simultaneously during one shuffling operation. When the glasses are shuffled, the marble doesn't travel from one glass to another: it moves together with the glass it was initially been put in.
After all shuffling operations Petya shows Vasya that the ball has moved to position t. Vasya's task is to say what minimum number of shuffling operations Petya has performed or determine that Petya has made a mistake and the marble could not have got from position s to position t.
If the marble can move from position s to position t, then print on a single line a non-negative integer — the minimum number of shuffling operations, needed to get the marble to position t. If it is impossible, print number -1.
-1
#include #include #include #include #include #include #include #include
Permutation p is an ordered set of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. We'll denote the i-th element of permutation p as pi. We'll call number n the size or the length of permutation p1, p2, ..., pn.
You have a sequence of integers a1, a2, ..., an. In one move, you are allowed to decrease or increase any number by one. Count the minimum number of moves, needed to build a permutation from this sequence.
Print a single number — the minimum number of moves.
Please, do not use the %lld specifier to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams or the %I64d specifier.
In the first sample you should decrease the first number by one and then increase the second number by one. The resulting permutation is (2, 1).
In the second sample you need 6 moves to build permutation (1, 3, 2).
贪心地从小到大排序;
#include #include #include #include #include #include #include #include
Permutation p is an ordered set of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. We'll denote the i-th element of permutation p as pi. We'll call number n the size or the length of permutation p1, p2, ..., pn.
Petya decided to introduce the sum operation on the set of permutations of length n. Let's assume that we are given two permutations of length n: a1, a2, ..., an and b1, b2, ..., bn. Petya calls the sum of permutations a and b such permutation c of length n, where ci = ((ai - 1 + bi - 1) mod n) + 1 (1 ≤ i ≤ n).
Operation 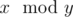 means taking the remainder after dividing number x by number y.
means taking the remainder after dividing number x by number y.
Obviously, not for all permutations a and b exists permutation c that is sum of a and b. That's why Petya got sad and asked you to do the following: given n, count the number of such pairs of permutations a and b of length n, that exists permutation c that is sum of a and b. The pair of permutations x, y (x ≠ y) and the pair of permutations y, x are considered distinct pairs.
As the answer can be rather large, print the remainder after dividing it by 1000000007 (109 + 7).
In the single line print a single non-negative integer — the number of such pairs of permutations a and b, that exists permutation c that is sum of a and b, modulo 1000000007 (109 + 7).
1800

#include #include #include #include #include #include #include #include
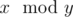 means taking the remainder after dividing number x by number y.
means taking the remainder after dividing number x by number y.